Is 84 Prime Or Composite

Prime Factorization Reckoner

Please provide an integer to find its prime factors besides equally a factor tree.

What is a prime number?

Prime number numbers are natural numbers (positive whole numbers that sometimes include 0 in sure definitions) that are greater than 1, that cannot exist formed past multiplying ii smaller numbers. An case of a prime number is vii, since it tin only be formed by multiplying the numbers one and 7. Other examples include two, 3, five, xi, etc.

Numbers that can exist formed with 2 other natural numbers, that are greater than 1, are called composite numbers. Examples of this include numbers similar, four, six, nine, etc.

Prime numbers are widely used in number theory due to the fundamental theorem of arithmetic. This theorem states that natural numbers greater than 1 are either prime, or can be factored every bit a product of prime numbers. As an example, the number threescore can be factored into a product of prime number numbers equally follows:

60 = v × iii × two × two

Equally tin be seen from the example above, there are no composite numbers in the factorization.

What is prime number factorization?

Prime factorization is the decomposition of a composite number into a production of prime numbers. There are many factoring algorithms, some more complicated than others.

Trial sectionalisation:

One method for finding the prime number factors of a composite number is trial partition. Trial division is one of the more basic algorithms, though it is highly tedious. Information technology involves testing each integer past dividing the composite number in question by the integer, and determining if, and how many times, the integer tin divide the number evenly. Every bit a simple example, below is the prime number factorization of 820 using trial division:

820 ÷ ii = 410

410 ÷ 2 = 205

Since 205 is no longer divisible past 2, test the next integers. 205 cannot be evenly divided past 3. iv is not a prime. It can all the same be divided by 5:

205 ÷ 5 = 41

Since 41 is a prime, this concludes the trial partition. Thus:

820 = 41 × 5 × 2 × 2

The products can also be written as:

820 = 41 × 5 × 2²

This is essentially the "beast force" method for determining the prime factors of a number, and though 820 is a simple example, it tin can get far more than tedious very quickly.

Prime number decomposition:

Another mutual way to comport prime number factorization is referred to as prime decomposition, and tin can involve the utilize of a factor tree. Creating a cistron tree involves breaking upwardly the composite number into factors of the composite number, until all of the numbers are prime. In the example below, the prime factors are establish by dividing 820 by a prime number factor, 2, then continuing to divide the event until all factors are prime. The example below demonstrates two ways that a factor tree tin be created using the number 820:

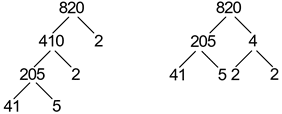
Thus, information technology tin be seen that the prime factorization of 820, in either instance, once again is:

820 = 41 × five × 2 × 2

While these methods work for smaller numbers (and there are many other algorithms), there is no known algorithm for much larger numbers, and it tin take a long catamenia of time for even machines to compute the prime factorizations of larger numbers; in 2009, scientists ended a project using hundreds of machines to cistron the 232-digit number, RSA-768, and it took two years.

Prime factorization of common numbers

The following are the prime number factorizations of some mutual numbers.

Prime factorization of 2: prime number number

Prime factorization of three: prime number

Prime factorization of iv: 2²

Prime factorization of 5: prime number number

Prime factorization of 6: ii × 3

Prime factorization of seven: prime number number

Prime factorization of viii: 2ⁱⁱⁱ

Prime factorization of 9: three²

Prime factorization of x: 2 × 5

Prime factorization of xi: prime number

Prime factorization of 12: 2² × iii

Prime factorization of 13: prime number

Prime factorization of 14: two × 7

Prime factorization of xv: three × five

Prime factorization of 16: ii⁴

Prime factorization of 17: prime number number

Prime number factorization of 18: ii × 3²

Prime number factorization of 19: prime number number

Prime factorization of 20: 2² × 5

Prime factorization of 21: 3 × 7

Prime factorization of 22: two × 11

Prime factorization of 23: prime number

Prime number factorization of 24: 2^three × 3

Prime factorization of 25: five²

Prime factorization of 26: 2 × xiii

Prime factorization of 27: three³

Prime factorization of 28: ii² × 7

Prime number factorization of 29: prime number

Prime factorization of thirty: 2 × 3 × 5

Prime number factorization of 31: prime number

Prime number factorization of 32: 2⁵

Prime factorization of 33: iii × eleven

Prime factorization of 34: 2 × 17

Prime number factorization of 35: 5 × seven

Prime factorization of 36: 2² × 3²

Prime factorization of 37: prime

Prime number factorization of 38: 2 × 19

Prime factorization of 39: 3 × thirteen

Prime factorization of forty: ii^three × v

Prime factorization of 41: prime number

Prime factorization of 42: ii × 3 × 7

Prime factorization of 43: prime number

Prime factorization of 44: 2² × 11

Prime factorization of 45: 3² × 5

Prime factorization of 46: 2 × 23

Prime factorization of 47: prime number

Prime number factorization of 48: 2⁴ × iii

Prime factorization of 49: 7²

Prime factorization of fifty: 2 × five²

Prime factorization of 51: 3 × 17

Prime factorization of 52: two^two × 13

Prime number factorization of 53: prime number

Prime factorization of 54: 2 × 3^three

Prime factorization of 55: v × eleven

Prime number factorization of 56: 2ⁱⁱⁱ × 7

Prime number factorization of 57: three × 19

Prime factorization of 58: 2 × 29

Prime factorization of 59: prime number

Prime number factorization of 60: 2^two × three × 5

Prime factorization of 61: prime

Prime number factorization of 62: 2 × 31

Prime factorization of 63: iii² × 7

Prime number factorization of 64: 2⁶

Prime number factorization of 65: 5 × 13

Prime factorization of 66: 2 × 3 × 11

Prime factorization of 67: prime

Prime number factorization of 68: 2² × 17

Prime number factorization of 69: 3 × 23

Prime factorization of 70: 2 × 5 × 7

Prime factorization of 71: prime number number

Prime number factorization of 72: twoⁱⁱⁱ × 3²

Prime factorization of 73: prime number

Prime factorization of 74: ii × 37

Prime number factorization of 75: three × 5²

Prime factorization of 76: 2ⁱⁱ × 19

Prime number factorization of 77: 7 × 11

Prime factorization of 78: ii × 3 × 13

Prime factorization of 79: prime number

Prime factorization of 80: 2⁴ × 5

Prime factorization of 81: 3^iv

Prime factorization of 82: ii × 41

Prime factorization of 83: prime number

Prime factorization of 84: 2ⁱⁱ × three × vii

Prime factorization of 85: five × 17

Prime factorization of 86: two × 43

Prime factorization of 87: three × 29

Prime factorization of 88: 2ⁱⁱⁱ × xi

Prime factorization of 89: prime number

Prime factorization of 90: 2 × threeⁱⁱ × five

Prime factorization of 91: 7 × 13

Prime number factorization of 92: two² × 23

Prime factorization of 93: 3 × 31

Prime factorization of 94: 2 × 47

Prime factorization of 95: v × xix

Prime factorization of 96: 2⁵ × 3

Prime factorization of 97: prime

Prime factorization of 98: 2 × 7²

Prime number factorization of 99: 3^two × 11

Prime factorization of 100: 2² × 5²

Prime factorization of 101: prime number

Prime factorization of 102: 2 × iii × 17

Prime number factorization of 103: prime number

Prime factorization of 104: 2³ × 13

Prime number factorization of 105: 3 × v × vii

Prime factorization of 106: two × 53

Prime factorization of 107: prime

Prime factorization of 108: 2² × 3^three

Prime factorization of 109: prime number

Prime factorization of 110: 2 × 5 × eleven

Prime factorization of 111: 3 × 37

Prime factorization of 112: 2⁴ × vii

Prime factorization of 113: prime number

Prime factorization of 114: two × 3 × 19

Prime factorization of 115: 5 × 23

Prime factorization of 116: 2² × 29

Prime factorization of 117: iii^two × xiii

Prime factorization of 118: ii × 59

Prime factorization of 119: seven × 17

Prime factorization of 120: two³ × 3 × five

Prime factorization of 121: 11²

Prime number factorization of 122: 2 × 61

Prime factorization of 123: 3 × 41

Prime number factorization of 124: 2² × 31

Prime factorization of 125: five³

Prime number factorization of 126: 2 × iii² × 7

Prime factorization of 127: prime

Prime number factorization of 128: 2⁷

Prime factorization of 129: 3 × 43

Prime factorization of 130: two × v × 13

Prime number factorization of 131: prime number

Prime factorization of 132: twoⁱⁱ × three × 11

Prime number factorization of 133: vii × nineteen

Prime number factorization of 134: 2 × 67

Prime factorization of 135: three³ × 5

Prime factorization of 136: ii³ × 17

Prime factorization of 137: prime number

Prime factorization of 138: 2 × three × 23

Prime number factorization of 139: prime number

Prime factorization of 140: 2² × five × 7

Prime factorization of 141: 3 × 47

Prime number factorization of 142: 2 × 71

Prime number factorization of 143: 11 × 13

Prime factorization of 144: 2⁴ × 3^two

Prime factorization of 145: 5 × 29

Prime factorization of 146: two × 73

Prime factorization of 147: 3 × seven²

Prime factorization of 148: two² × 37

Prime factorization of 149: prime number

Prime number factorization of 150: ii × 3 × v²

Prime factorization of 200: 2³ × 5²

Prime factorization of 300: 2ⁱⁱ × three × 5^two

Prime factorization of 400: two^iv × 5²

Prime factorization of 500: 2ⁱⁱ × 5ⁱⁱⁱ

Prime factorization of 600: twoⁱⁱⁱ × 3 × v²

Prime factorization of 700: 2ⁱⁱ × five² × 7

Prime factorization of 800: 2⁵ × five²

Prime factorization of 900: two² × three² × 5ⁱⁱ

Prime factorization of 1000: 2ⁱⁱⁱ × 5³